世界上最完美的公式--欧拉公式

在数学历史上有很多公式都是欧拉(Leonhard Euler公元1707-1783年)发现的，它们都叫做欧拉公式，它们分散bai在各个数学分支之中。

欧拉方程是迄今为止最美丽的数学公式。它简单、优雅，汇集了一些最重要的数学常数，并有奇怪的数学和物理解释。

让我们仔细检查一下。

这个公式

欧拉的标志公式就是本文标题中显示的那个。让我们再来看看这里：

自从这个三项公式被创造出来以来，它就一直让全世界的数学家们感到惊讶，因为它建立了包含在其中的不同元素和它的不同解释之间的惊人联系。

在这篇文章中，我们将试着揭开欧拉身份的神秘面纱，并展示它的神奇之处。

在那之前，让我们看看这个公式是怎么来的。

欧拉恒等式的历史。

1714年，英国物理学家和数学家罗杰·柯特用一个公式建立了对数、三角函数和虚数之间的关系。

20年后，莱昂哈德欧拉(Leonhard Euler)得出了同样的公式，但使用的是指数函数而不是对数。这两个公式以及如何从一个到另一个在下面的图中进行了说明。

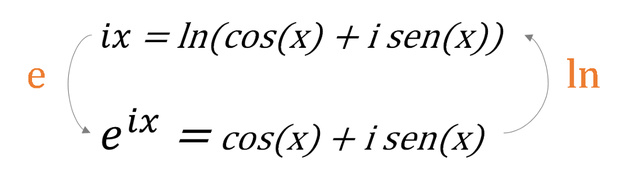
1714年的Roger’科特斯方程(上)，1748年的欧拉公式(下)值得注意的是，没有一个作者看到他们的公式的几何内涵，我们将在后面讨论。

现在，如果我们详细说明欧拉公式x =π的值，我们得到了著名的欧拉恒等式。

通过用x代替Euler公式中的π，我们得到Euler的恒等式让我们分别研究一下这个公式中涉及的不同元素。

首先也是最重要的人物是莱昂哈德·欧拉（Leonhard Euler）。他对数学和物理世界的贡献从图形和数论到流体力学。